今回は、WACC構成要素の1つであるβの算出方法について書きます。実務的にはBloombergやCapital IQ等のデータベースから抽出しますが、理論は理解しておいた方が良いので自力で計算する方法も押さえておきましょう!
β(ベータ)とは
βは、市場全体が動いた時に特定の銘柄がどの程度連動して動くかを示す指標になります。市場全体と全く同じ動きをすれば「1」となり、市場全体の動きに対して感度が高い銘柄は1を超える値に、感度が低い銘柄は1より低い値をとります。例えば製薬会社や食品会社等、私たちが生活する上で必要な製品/サービスを取り扱っているような会社のβは低くなる傾向にあります。
βの算出ステップ
フィナンシャル・アドバイザリー業務やバリュエーション業務に従事している方は算出できて欲しいところですが、普段データベースに頼っているため、いざやってみてと言われると意外と苦戦する人もいると思います。そういう方は復習がてら読んで思い出してみてください。では早速見ていきましょう!
β算出の前提
当記事では、日本を代表する自動車メーカーであるトヨタ自動車を例に進めたいと思います。したがって、比較する市場は日本株式のベンチマークである東証株価指数TOPIXとします。
また、βの測定期間の採り方は色々ありますが、今回は実務的にもよく見かける5年月次で進めます(算定基準日は2020年12月末とします)。
ステップ1:5年分の月次株価データを取得
株価データが取れればソースは何でも良いのですが、私はYahoo!ファイナンスを使用します。
トップページに飛んだらページ上部の検索バーに銘柄名を入れて「株価検索」します。

対象銘柄を選択し、対象銘柄ページに遷移したら時系列タブを選択します。

株価の時系列データの下に次のようなボックスがあるので、そこに5年分の月次データが取れるように条件をセットし、表示を押下します。

次の通り、5年分の月次データが複数ページに渡って表示されたと思います。
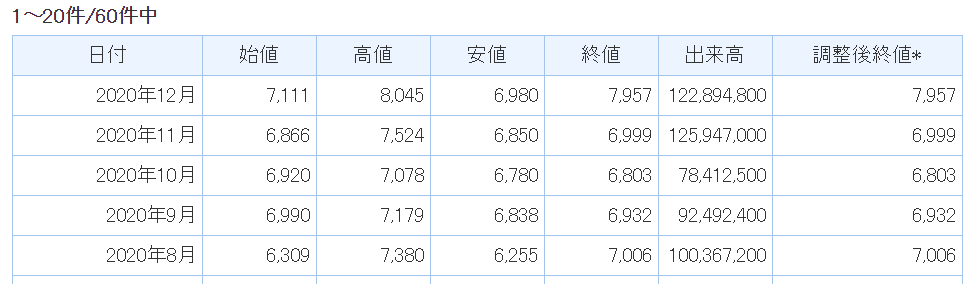
これをコピーしてエクセルに貼り付け。。。と言いたいところですが、コピーしてそのまま貼るとこんな感じになります。1セルに全データ突っ込まれちゃうんですね。。。

なので一旦メモ帳に貼ってください。私はメモ帳に全部の株価を貼ってから全選択⇒コピーしてエクセルに移します(都度貼り付けても構いません。趣味の領域です)

トヨタ自動車とTOPIXがこんな感じで貼れたら次のステップに移行します。
ステップ2:取得データ終値の月次増減を計算
特に説明は要らないと思いますが、1ヶ所抜き出して例示しておくと以下の通りです。
増減率 = 2020年12月株価終値/2020年11月株価終値 – 1
これを各期間で計算します。今回5年月次で60データあるので、上記の計算結果としては59個並びます。
ステップ3:エクセル機能を利用してβを算出
ステップ3は2通りのやり方があります。1つは関数を使って算出する方法、もう1つはグラフを作って出す方法です。
方法①:エクセル関数の利用
まずはエクセル関数を利用したβの算出方法を見ていきましょう!
βの算出方法
βをシンプルな式で表すと、
β = 特定銘柄のリターン/市場全体のリターン
となります。特定銘柄の動き(変数y)を市場全体(変数x)の動きから予測する単回帰分析(一次式:y = α + βxを利用)をおこなう場合、最小二乗法を用いて次のように表すことができます。
β = xyの共分散/xの分散
要するにxyの共分散を求める式とxの分散を求める式があれば、βは求められるということです!そして流石エクセルです、ちゃんとそれらを求める式が用意されています。
xyの共分散 = COVARIANCE.P(yの範囲 , xの範囲)
xの共分散 = VAR.P(xの範囲)
今回の例に適用すると、次の通りになります。くどいようですがβは市場全体に対して特定銘柄がどう増減するかを表す指標です。なので今回の例では、yにトヨタ自動車、xにTOPIXを対応させます。関数の引数に入れるx, yそれぞれの範囲はステップ2で算出した月次増減のデータになります。

2020年12月末を基準日としたトヨタ自動車の5年月次βは1.0333となりました。ほぼTOPIXと同じ動きをする銘柄ということですね!
決定係数の算出方法
βの計算としては上記で良いのですが、当該βが統計上有効かどうかを検討する必要があります。実務上決定係数(相関係数の二乗)が0.1以上であれば有効値とみなしているケースが多いように思います。
決定係数は相関係数の二乗なので、まず相関係数を求めていきます。相関係数は次式で求めることができます。
相関係数 = xyの共分散/(xの標準偏差 * yの標準偏差)
βの算出時にxの分散を算出しているので、xの標準偏差の計算に活用しましょう。xの標準偏差を求める式もエクセル上存在しますが、工夫して利用できるものは利用しちゃいましょう!分散は「分散 = 標準偏差^2」という式で表すことができるため、標準偏差は分散の平方根として求めることができます。xと同様にyについても計算します。計算要素がそろったら上式に当てはめて相関係数を計算します。その後は相関係数を二乗すれば決定係数が求められます。トヨタ自動車の例だと次のようになります。

決定係数は0.5971ということで0.1以上の値を取っています。したがって、βが統計上問題なく利用できる数値であることが確認できました。
β及び決定係数を直接求める関数
数学教師のようなことを言いますが、理論を理解した上で便利な関数を使用するのは良いと思っています。なので、βや決定係数を直接的に求める方法もシェアしておきます。
SLOPE関数
SLOPE関数は回帰直線の傾きを求める関数で、以下のような式で求めることが可能です。
= SLOPE(yの範囲 , xの範囲)
INTERCEPT関数
単回帰分析に用いる一次式「y = α+βx」の傾きを求めたので、ついでに切片αを求める式にも触れておきます。この後グラフを見ていきますが、そのグラフ切片の値との一致をご確認ください。
= INTERCEPT(yの範囲 , xの範囲)
α:市場全体のリターンに対する特定銘柄の超過リターンを表す指標です。CAPM等のベンチマークと比較した場合、そのモデルから得られる均衡収益率と特定銘柄に対する期待収益率の差分がαであり、要するに、特定銘柄の「特性」に帰属する超過収益率を指します。
RSQ関数
RSQ関数は、既知のx,yを通る回帰直線に対する相関係数の二乗を求める関数です。
= RSQ(yの範囲 , xの範囲)
結果を貼っておきますが、上で求めたβ及び決定係数と一致していることが確認できます。

方法②:エクセルグラフの利用
次にグラフを作成し、回帰直線の傾きからβを確認する方法です。
手順というほどのものでもないので簡単に書きますが、ステップ2で計算した増減率のデータ(59×2の合計118データ)をレンジで選択し、エクセルの挿入タブのグラフから散布図を選択してOKを押下します。
グラフが表示されたら、グラフ要素から「近似曲線」にチェックを入れます。
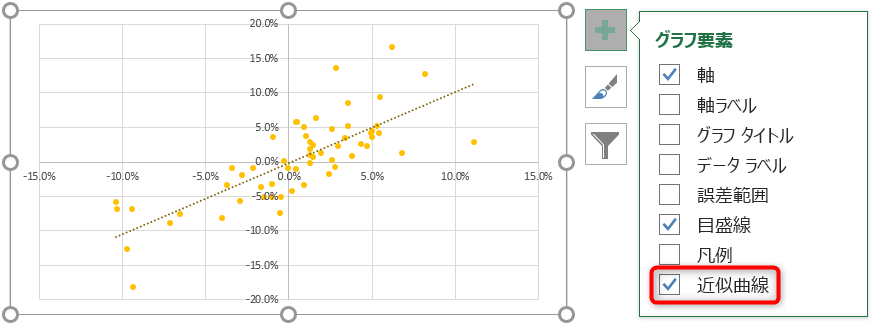
出現した直線をダブルクリックすると、近似曲線の書式設定タブが出てきます。そのタブにある「グラフに数式を表示する」と「グラフにR-2乗値をを表示する」にチェックを入れると、回帰直線の式と決定係数がグラフ上に出現します。
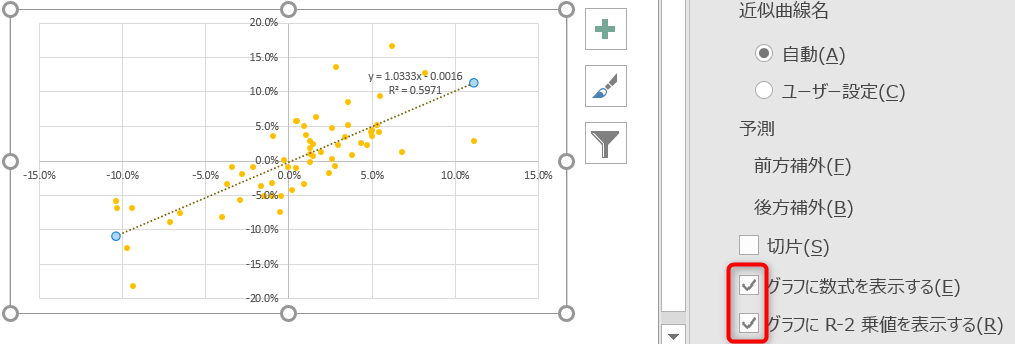
少し見づらいので表示された式を書き出してみると、
y = 1.0333x – 0.0016
R² = 0.5971
α、β、決定係数の全てにおいて、エクセル関数を用いた場合との結果の一致を確認できました!
ステップ4:修正βの算出
ステップ3で算出したβは、修正βと区別して未修正βと呼ばれます。何が未修正?ということについてはこの後説明していきますが、未修正βをWACC算定に使用すること自体は誤りではありません。ただ、実務上修正βが使われているケースの方が多いため、ここではステップ4として紹介することにしました。
修正βは以下の式で計算することが可能です。
修正β = 未修正β * (2/3) + (1/3)
未修正βに2/3を乗じて1/3を加算するこの調整は、企業が事業継続していけばいずれは市場平均を表す「1」に収斂していくという考え方に基づくものです。実際に計算してみるとより分かりやすいのですが、今回の例をでいくと次のようになります。少し「1」に近づいていますよね!
修正β = 1.0333 * (2/3) + (1/3) = 1.0222
当記事の作成に使用したβ算定ファイルはSTORE上でダウンロード可能ですので、より理解を深めたい方は是非ご活用ください!
まとめ
いかがでしたか?統計に馴染みがないと、なかなかしっかり理解するのは大変ですよね。これからフィナンシャル・アドバイザリー業務やバリュエーション業務に従事される方はこの機会にしっかり理解されておくことをオススメします!
以上です!














コメント